Pipelines and engines are studied under the thermal stress during operation. With the calculated ratios obtained, it is possible to settle practical issues in operation in order to increase the reliability and safety of equipment. To this end, it is first necessary to investigate the thermal mode of the pipeline, the engine for the planned period by the operations control centre. At the same time, the equipment with the average temperature at a certain time of the year exceeding the design value should be identified. In addition, the equipment concerning the nature of jamming should be studied at the sections specified in such a way. In case of identifying the jammed sections based on the above calculated ratios by thermal deformation and stressing the necessary value of movement of the sections, it should be determined that the actual voltage does not exceed the permissible level.
Received 7 November 2015; accepted 9 January 2016; published 12 January 2016
In the operation of one of the main types of machines in the oil, gas and energy sectors pipelines are known pipelines and engines associated with a reduction of reliability and safety [1] [2] . One of the reasons that create unsafe operational conditions for machines in that case is thermal stress, deformation, jams in the machines (rods, pipes and engines) [3] [4] .
In connection with this, the article addresses the issue based on the thermodynamic ratios and thermal conductivity to build design ratios by determining the occurring thermal stresses that cause abnormal and unsafe conditions for pipelines, rods and heat engines. The obtained solutions are made available for use in the inspecting, diagnosing or during the technical examination of machines in question [5] [6] .
2. Settlement Ratios of Thermodynamics and Heat Transfer for the Thermal Stress of the Equipment
Thermal stress occurs in engineering. In case of gas pipeline systems, thermal stress can occur in a pipeline particularly in the jammed sections, gas compressor units, pistons, turbines etc. [1] [3] . Since the gas temperature in the pipeline section is substantially above the temperature of the soil, an intensive heat exchange between the soil and pipe takes effect. The temperature along the pipeline drops but due to the high coefficient of heat transfer from gas to the wall, the wall temperature is practically the same as the gas temperature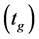
. Since the pipeline is laid at a different temperature
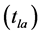, thermal stresses and deformations will inevitably arise due to relative elongations in the linear part of the gas pipeline:
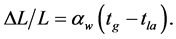(1)
where ΔL―change of length of the pipeline L; αw―coefficient of thermal, linear expansion of the pipeline and of the rode.
Due to pipeline jamming (soil or dead spots) the linear expansion can be completely destroyed. Compression stress takes place:
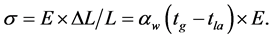(2)
where E―the elasticity modulus of the rod material and of the pipe material.
These additional stresses are the greatest value in the initial section of the gas pipeline, at the output of the compressor station CS where gas has the highest temperature. A rational way to combat the thermal stress is to pre-cool gas before it enters the pipeline [2] [4] . Under certain conditions, such as permafrost gas pre-cooling to low temperatures may become the only means of gas transport. In the case of the use of special coolers, unlike air coolers, for example, the compression- or absorption-type chillers, it is expedient to install them before blo- wers prior to the compression process at the compression station input. It is possible for air coolers during the cold season, when there is a considerable difference in temperature between gas and ambient air temperature while the cooled gas temperature with the help of air coolers does not reach the dew point. In this case, it is possible to either gain in the power supplied on compressing the gas, or increase the capacity of the compressor station reaching 10% or more.
Changing the length of the rod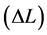 
is subject to the following law:
(3)
where L―rod length;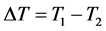
―temperature change.
If the elements of bodies, structures freely expand or constrict, i.e. are not fixed, the temperature changes do not cause stress. The change in length caused by temperature change
, is eliminated by the influence of stress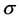 
according to the equation:
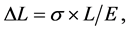(4)
On the basis of the last two equations it follows:
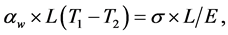(5)
from where:
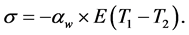(6)
If lengthening or shortening the rod is limited only in part, the last equation can be written as follows:
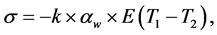(7)
where k―factor depending on the nature of consolidation.
The calculated ratios presented above can be used to conduct the technical inspection of pipeline sections concerning thermal strains and stresses and determine the nature of jamming. In case of clamped areas are identified on the basis of the above calculated ratios in terms of thermal strains and stresses, it may be possible to determine the necessary amount of transfer of the sections based on the condition that the actual voltage does not exceed the permissible one.
3. Examples of the Calculated Temperature Stresses in Pipelines and Heat Engines
3.1. Example 1
A steel rod 50 cm long is fitted between the two walls without any preload at 32˚C. What the tension in the rod at 35˚C is going to be. How this tension will change, if the wall moves by ΔL = 0.25 mm from one another. The thermal expansion coefficient and the modulus of elasticity of the material of the rod are respectively equal to αw = 12.5 × 10−6 ˚C−1 and E = 2.04 × 106 bar.
We first define the tension in the rod without taking into account the nature of fixing:
(8)
Given the nature of fixing the tension in the rod becomes equal to:
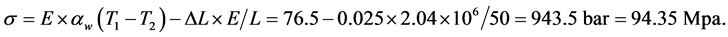(9)
The coefficient, which depends on the nature of fixing the rod, is determined by the following formula:
(10)
In view of the obtained values of the coefficient, the tension in the rod will fall sharply.
3.2. Example 2
A steel pipe is clamped at a section with the length L = 1000 m without any preload at an average temperature T1 = 23˚C. What voltage will be in the pipe with an increase in its temperature to T2 = 26˚C, which is due to its increased load. How this tension will change in the pipeline, if its clamped ends will at a distance of 0.5 m. The thermal expansion coefficient and modulus of elasticity of the pipe material are respectively equal to αw = 12.5 × 10−6 ˚C−1 and E = 2.04 × 106 bar.
First we determine the voltage at a given section of the pipeline when its temperature changes taking into account his clamping:
(11)
In view of the possibility of moving the clamped ends of the pipe by 0.5 m the tension at the considered section will be determined from the following equations:
(12)
from where
(13)
The coefficient, which depends on the nature of the pipeline’s clamping, will be determined by the following formula:
(14)
Since the clamped ends of the pipe can be moved, it is possible to reduce the tension at the considered section to a value that does not exceed the allowable stress of the pipe material. Thus, the possibility of moving the clamped ends of the pipe to the desired value makes it possible to prevent rupture and destruction of the pipeline [6] [7] .
The objectives of the technical inspection of pipeline sections by the thermal deformation and stress the nature of clamping. If there are any clamped areas on the basis of the above calculated ratios of thermal deformations and stresses, it may be necessary to determine the amount of movement of the sections based on the condition that the actual stress does not exceed the permissible one.
3.3. Example 3
According to the pipeline temperature data, for the coming period is set exceeding the mean pipe temperature by 5 degrees at the section with the length of 10,000 km. To determine the value by which it is necessary to shift the considered section by its ends, so that the actual stress by the thermal deformations in the pipeline does not exceed the permissible σ = 720 Mpa. The thermal expansion coefficient and modulus of elasticity of the pipe material are taken to be equal, respectively αw = 12.5 × 10−6 ˚C−1 and E = 2.04 × 106 bar = 0.204 × 106 Mpa.
The above problem is an example of this kind of problems of technical inspection of pipelines by thermal deformation and stress, which are offered for use in the inspection, diagnosis, or during the technical examination of pipelines [8] [9] .
3.4. Example 4
Determination of the Actual Thermal Stresses in the Cylinder Group Induced by Abnormalities in the Engine
The presented problem is associated with the definition of thermal deformations that can cause scratching in the moving parts of the engine cylinder. The initial data set as follows: D―diameter of the cylinder; b―the gap between the piston and cylinder; the piston material and its characteristics: αw―the coefficient of the linear thermal expansion; E―modulus of elasticity.
Calculations are made for a diesel engine with the compression ratio equal to
. The rest of the original data and additional conditions of the problem are given in the course of solving. The solution of the problem begins by determining the maximum temperature of the operating procedure for the engine in the following sequence. The molecular weight of the working mixture is determined by the composition of the combustion products: oxygen-O2 = 0.08; nitrogen-N2 = 0.72; carbon dioxide-CO2 = 0.14; water vapour-H2O = 0.06:
(15)
The characteristic constant of the gas mixture:
(16)
The first average mass isobaric and isochoric heat capacities and adiabatic indices:
(17)
(18)
(19)
Then the thermodynamic parameters at each point of the operating procedure are calculated (points: 1) the beginning of the compression process; 2) the beginning of the supply of heat to the working medium―the beginning of the combustion process; 3) and 4) beginning and the end of the enlargement process of the working medium in the cylinder) [5] [10] . Point 1: the initial data-p1 = 105 Pa; t1 = 30˚C; from the equation of state of this point we can obtain the specific volume:
(20)
Point 2: the initial data-
, from where v2 = 0.869/12.5 = 0.070 m3/kg; rate of expansion n = 1.32; from the equation of:
(21)
we derive the pressure at the end of the compression process:
(22)
From the equation of state for point 2 we obtain the value of the absolute temperature:
(23)
Point 3: the initial data-
; from where
.
From the corresponding equation of state we evaluate the temperature of the working medium of the engine at the beginning of the expansion process:
(24)
Point 4: at 
from the equation of the expansion process calculated is the temperature at the end of the process:
(25)
The gas temperature at the end of the expansion process is determined from the equation of state:
(26)
Thus, based on thermodynamic calculations the maximum temperature of the working medium of the engine will be equal to the temperature at the end of expansion:
.
Further, the structural and technological parameters are included as the initial data in the calculations. Cast iron is taken as piston material, for which the thermal expansion coefficient and modulus of elasticity are respectively as follows: 
and E = 10 bar; the piston diameter D = 40 cm = 0.4 m; maximum and minimum clearances between the piston and cylinder, respectively, in the upper and lower parts of the piston are recommended equal:
(27)
(28)
In the operation, the real and maximum temperature of the engine exceeds the maximum and design cycle temperature calculated using the formula (24). The growth of the real maximum temperature may occur due to all kinds of losses occurring in the running engine, high loads, deteriorating technical condition, disturbance of the cooling mode etc. [11] [12] . In this regard, the following values of the possible, actual and maximum temperatures in the engine are set:
(29)
The thermal elongations are calculated in the case of extensions of the minimum clearance b2 = 0.4 mm = 0.04 cm; piston diameter
.
The phenomenon of scuffing in the cylinder occurs under the condition when the temperature elongation becomes equal to or greater than the minimum clearance between the piston and cylinder.
A change in the diameter of the piston caused by an increase in temperature of the combustion products is computed for the above-taken three maximum temperature values based on the known formula:
(30)
Then, calculated are the real gaps formed for three adopted and maximum temperatures caused by different operating conditions:
(31)
The obtained results indicate that in the risen actual temperature in the engine cylinder with respect to the maximum design temperature of the cycle by 100 degrees, the conditions for scuffing of the cylinder face, which correspond to the second value of the adopted maximum temperature value in the engine cylinder, are created. If this difference is exceeded above 100 degrees, dangerous failures in the engine are possible. Thus, in the third case, when the difference between the actual engine temperature and maximum design temperature of the cycle is equal to 150 degrees, a serious engine breakdown associated with piston seizure in the cylinder may occur.
Let us determine the temperature stress in the considered three cases of the maximum temperature in the engine by the previously given formula:
(32)
The derived results indicate that when the temperature inside the engine cylinder is exceeded relative to the maximum design cycle temperature by 100 degrees (whether in ˚C or ˚K), there is a tension in the engine exceeding the permissible temperature equal to 800 - 900 bar for cast iron.
Similar calculations can be made for internal combustion engines made of other materials. For example, if a piston is made of aluminium, the thermal expansion coefficient and elastic modulus of the material will be equal respectively to: 2.2 × 10−5 ˚C−1 and 7.5 × 105 bar; the maximum and minimum clearances between the piston and cylinder of the engine are recommended within the following limits: 
and 
.
The Chapter “Settlement ratio of thermodynamics and heat transfer for the thermal stress of equipment” provides the corresponding formulas to carry out the task of the technical inspection of pipeline sections and heat engines by thermal deformation and stress and to determine the nature of clamping.
The Chapter “Examples of the Calculated Temperature Stresses in Pipelines and Heat Engines” considers two groups of tasks to control the temperature mode of pipelines and heat engines.
Example 1 concerns the thermal stresses and deformation in the rods. In case of any clamped areas based on the above calculated ratios by thermal strains and stresses determined is the required value of movement of these areas based on the condition that the actual stress does not exceed the permissible one.
Examples 2 and 3 address the issues related to the technical inspection of pipelines for thermal strains and stresses based on which practical recommendations for use during the inspection, diagnosing or technical examination of pipelines and ensuring the safe operation of pipelines are presented.
Example 4 addresses some issues devoted to control the temperature mode of the cylinder group to provide a reliable and safe operation of internal combustion engines trouble-free.
*Corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Cite this paper
http://www.scirp.org/Journal/paperinformation.aspx?paperid=62669