Posted on 8th Sep 2019
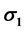 in the circumferential or hoop direction and
in the circumferential or hoop direction and 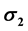 in the longitudinal or axial direction. A case study of internal pressure developed in a soda can was determined by measuring the elastic strains of the surface of the soda can through strain gages attached to the can and connected to Strain indicator Vishay model 3800.
in the longitudinal or axial direction. A case study of internal pressure developed in a soda can was determined by measuring the elastic strains of the surface of the soda can through strain gages attached to the can and connected to Strain indicator Vishay model 3800.


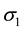 and
and 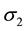 acting on the side faces of this element. No shear stresses act on these faces because of the symmetry of the vessel and its loading. Therefore, the stresses
acting on the side faces of this element. No shear stresses act on these faces because of the symmetry of the vessel and its loading. Therefore, the stresses 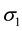 and
and 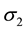 are principal stresses. Because of their directions, the stress
are principal stresses. Because of their directions, the stress 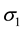 is called the circumferential stress or the hoop stress, and the stress
is called the circumferential stress or the hoop stress, and the stress 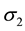 is called the longitudinal stress or the axial stress. Each of these stresses can be calculated from static equilibrium equations.
is called the longitudinal stress or the axial stress. Each of these stresses can be calculated from static equilibrium equations.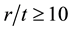 with
with 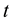 being uniform and constant
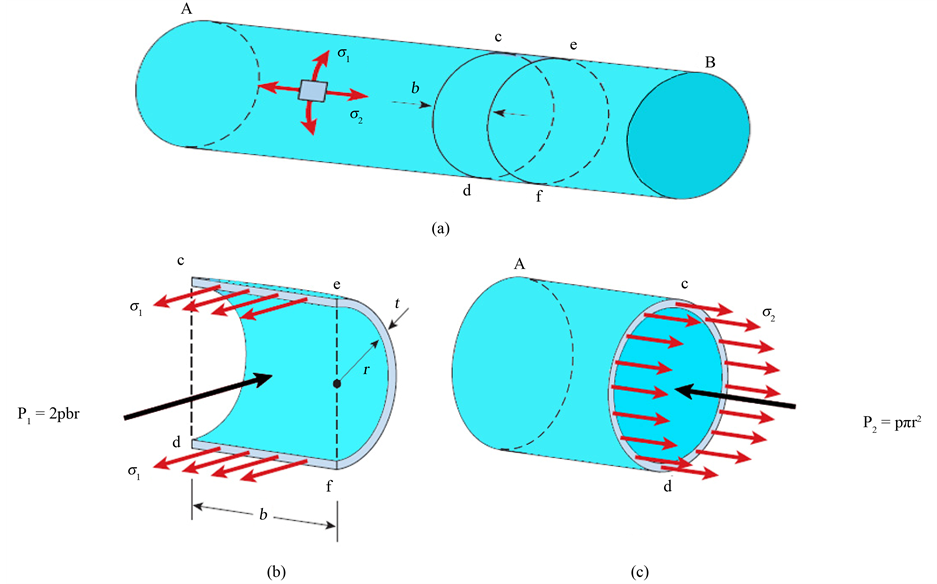
being uniform and constant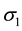 , make three sections (cd and ef) perpendicular to the longitudinal axis and distance
, make three sections (cd and ef) perpendicular to the longitudinal axis and distance 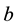 apart (Figure 3(a)); and a third cut in a vertical plane through the longitudinal axis of the tank. The resulting free body diagram is shown in Figure 3(b). Acting on the longitudinal cut (plane cefd) are the circumferential stresses
apart (Figure 3(a)); and a third cut in a vertical plane through the longitudinal axis of the tank. The resulting free body diagram is shown in Figure 3(b). Acting on the longitudinal cut (plane cefd) are the circumferential stresses 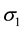 and the internal pressure
and the internal pressure .
. acting in the wall of the vessel have a resultant equal to
acting in the wall of the vessel have a resultant equal to , where
, where  is the thickness of the wall. Also, the resultant force
is the thickness of the wall. Also, the resultant force  of the internal pressure is equal to
of the internal pressure is equal to , where
, where  is the inner radius of the cylinder. Hence, we have the following equation of equilibrium:
is the inner radius of the cylinder. Hence, we have the following equation of equilibrium:
 (1)
(1) and an internal pressure
and an internal pressure , the formula may be expressed as:
, the formula may be expressed as: (2)
(2) is obtained from the equilibrium of a free body diagram shown in Figure 3(c). The stresses
is obtained from the equilibrium of a free body diagram shown in Figure 3(c). The stresses  acts longitudinally and have a resultant force equal to
acts longitudinally and have a resultant force equal to 
 . The resultant force
. The resultant force  of the internal pressure is a force equal to
of the internal pressure is a force equal to . The equation of equilibrium for the free body diagram is
. The equation of equilibrium for the free body diagram is
 , lead to the following formula for the longitudinal stress in a cylindrical pressure vessel:
, lead to the following formula for the longitudinal stress in a cylindrical pressure vessel: (3)
(3) and an internal pressure
and an internal pressure , the formula may be expressed as:
, the formula may be expressed as: (4)
(4) (5)
(5) and
and  at the outer surface of a cylindrical vessel are shown on the stress element of Figure 4(a). The element is in biaxial stress (stress in z direction is zero).
at the outer surface of a cylindrical vessel are shown on the stress element of Figure 4(a). The element is in biaxial stress (stress in z direction is zero).
 and
and  axes, respectively:
axes, respectively:

 (6)
(6)

 ,
,  , and
, and  axes, are
axes, are (7)
(7) (8)
(8) (9)
(9) is very large (thin walled), the term
is very large (thin walled), the term  can be disregarded, and the equations are the same as the stresses at the outer.
can be disregarded, and the equations are the same as the stresses at the outer. we cut the sphere into two hemispheres as shown in Figure 5. The free-body diagram gives the equilibrium condition
we cut the sphere into two hemispheres as shown in Figure 5. The free-body diagram gives the equilibrium condition , hence
, hence (10)
(10) ,
,  and
and  the spherical geometry is twice as efficient in terms of wall stress.
the spherical geometry is twice as efficient in terms of wall stress.

 and the hoop stress
and the hoop stress  (Figure 7). The longitudinal stress is a result of the internal pressure acting on the ends of the cylinder and stretching the length of the cylinder as shown in Figure 8. The hoop stress is the result of the radial action of the internal pressure that tends to increase the circumference of the can.
(Figure 7). The longitudinal stress is a result of the internal pressure acting on the ends of the cylinder and stretching the length of the cylinder as shown in Figure 8. The hoop stress is the result of the radial action of the internal pressure that tends to increase the circumference of the can. where:
where: ―internal pressure (psi)
―internal pressure (psi)




 (11)
(11) (12)
(12) ―modulus of elasticity or Young’s modulus (psi)
―modulus of elasticity or Young’s modulus (psi) ―Poisson’s ratio
―Poisson’s ratio ―hoop strain (in/in)
―hoop strain (in/in) ―longitudinal strain (in/in)
―longitudinal strain (in/in) (13)
(13) (14)
(14) (15)
(15) (16)
(16)
 &
& ) of the external surface of the soda can was determined through strain gages attached to the can surface and connected to a strain indicator. The longitudinal stress, hoop stress, and the internal pressure were determined from equations of generalized Hooke’s law for stress and strain. Small varia-
) of the external surface of the soda can was determined through strain gages attached to the can surface and connected to a strain indicator. The longitudinal stress, hoop stress, and the internal pressure were determined from equations of generalized Hooke’s law for stress and strain. Small varia-